how to draw 3d graph in r
Make beautiful 3D plots in R — An Enhancement to the Storytelling
Examples along with data interpretation
![]()

Why data visualization? When we work with statistics, no thing what data we are processing, what models we are using, data visualization is ever an inevitable function of the work. Sometimes we might merely make graphs mechanically and underestimate the importance of visualization. In fact, the visualization of the data not only makes the data easier to digest but also tells us more than than the data in text form and descriptive statistics. This is demonstrated past Anscombe's quartet.
Why 3D? Sometimes a 2nd plot (or multiple of them) can contain enough information we need, just a 3D plot is usually more intuitive since the 3D infinite is where nosotros reside. This is like the 2D project of a map, or atlas, which are what we usually meet in geography textbooks, but a globe is e'er more than pleasant to use — more fun, more intuition. As well, in statistics, we oft encounter higher dimensional spaces (larger than 3 dimensions) and 3D visualization can assistance united states of america with generalizing in higher dimensional spaces.
In this commodity, some useful types of 3D plots will be introduced, namely, 3D surface plot, 3D line plot and 3D scatter plot, and they will be implemented using libraries plotly or rgl. Also, we volition have a look at the interpretation of the graphs — we should know what practise the graphs mean since we are not just making nice pictures.
3D surface plot

The 3D surface plot made using the plot_ly function in the plotly library is perfect for visualizing geographic data. Using the code snippet from the documentation we can draw a quite realistic volcano out of the congenital-in dataset volcano. This information is very easy to interpret. The data set contains the topologic information on Auckland'south Maunga Whau Volcano, in the course of a 61 past 87 matrix. Each chemical element in the matrix is the height of the volcano in a 10 by 10 grid. Therefore, the outcome of the plot is the shape of the volcano. Non only the geographic information (height), but we can also employ it to correspond density, e.g. probability density. Firstly we generate a matrix of a probability distribution.
# simulate articulation probability distribution (normal)
num.rows <- threescore
num.cols <- 60 simulate <- function(n.row, n.col) {
# initiate the matrix
prob.n <- matrix(0, nrow=num.rows, ncol=num.cols)x.seq <- seq(i, due north.row)
y.seq <- seq(i, n.col)xx <- dnorm(x.seq, hateful=n.row/2, sd=12)
for (i in i:n.row) {
y <- dnorm(i, mean=northward.row/ii, sd=12)
res <- simulate(num.rows, num.cols)
prob.northward[i,] <- y * twenty
}
prob.n;
}
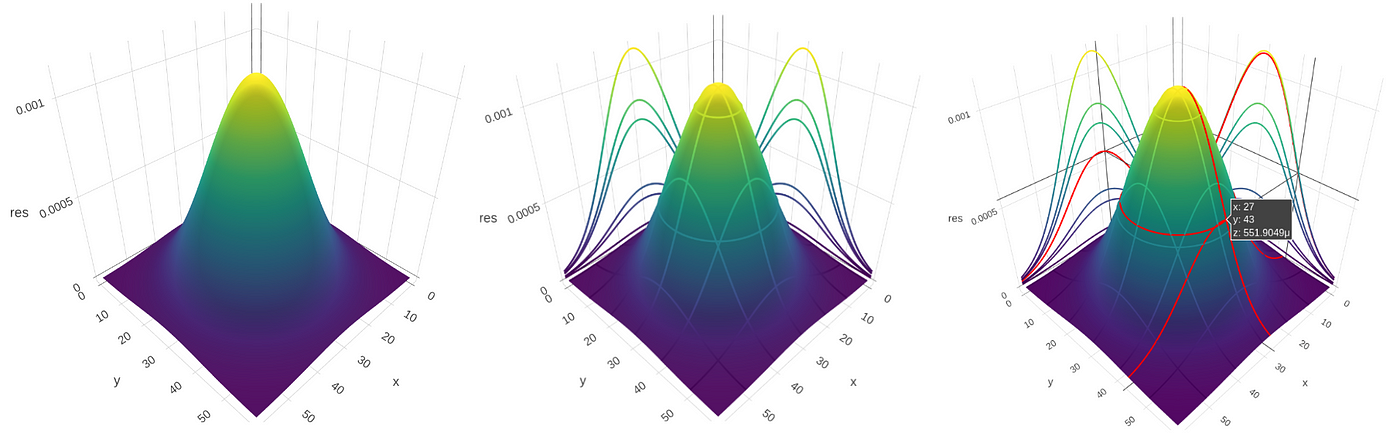
In this example, we simulate a joint probability of two normally distributed independent variables. We can use the following lawmaking to plot the graph, which will output Effigy 1.two (a)
# 3D plot of joint probability distribution without projection
fig.n <- plot_ly(z = ~res)
fig.n <- fig.northward %>% add_surface()
fig.n Or we can add projections to the x-z and y-z plane, this is set via the aspect contour.
# add projection
fig.nc <- plot_ly(z = ~res,
contours = list(
z = listing(
show=TRUE,
usecolormap=TRUE,
highlightcolor="#ff0000",
projection=list(z=Truthful)
),
y = list(
show=TRUE,
usecolormap=TRUE,
highlightcolor="#ff0000",
project=listing(y=TRUE)
), x = list(
evidence=True,
usecolormap=TRUE,
highlightcolor="#ff0000",
project=list(x=TRUE)
)
)
)
fig.nc <- fig.nc %>% add_surface()
fig.nc
The highlightcolor parameter determines the highlight color of the contours on the graph when hovering over the graph. In this instance, information technology'due south set to be scarlet. What does the graph tell us? The x and y axes denote the random variables X and Y, which accept normal distribution. The z-centrality shows the joint probability of Ten and Y — the probability of X and Y taking on item values (P(X=x and Y=y)), this determines the pinnacle of the "hill" in Effigy two.2. In our example, since X and Y are independent, P(10=x and Y=y) = P(Ten=ten)P(Y=y) according to the definition of independence. If X and Y accept different standard deviations, one of the projections will exist wider and the other volition exist narrower, and the cantankerous-section of the hill will be an ellipse, instead of a circumvolve.
Just nosotros need to exist careful nigh the meaning of the projection on the x-z and y-z planes. Information technology might seem like that they are marginal probabilities of Ten and Y, simply in fact, they are not. The projections just tell us the corresponding value of P(X=x and Y=y) with regard to Ten and Y. All the same, the marginal probability of X or Y should be the sum along rows or columns (retrieve about the table of marginal probability).
As well, we tin utilize a vector of color codes to define custom colors using the colors aspect. In Figure 1.3 the color templates are generated from coolors.
color.vec2 <- rev(c("#F2DC5D", "#F2A359", "#DB9065", "#A4031F", "#240B36"))
# color.vec2 <- rev(c("#F7AEF8", "#B388EB", "#8093F1", "#72DDF7", "#F4F4ED"))
fig.n2 <- plot_ly(z = ~res, colors=color.vec2)
fig.n2 <- fig.n2 %>% add_surface()
fig.n2 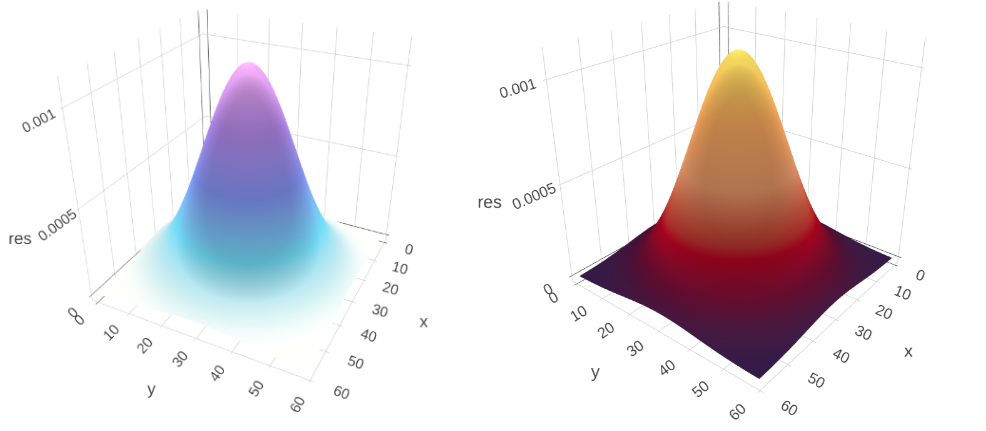
3d line plot and waterfall plot
3D line plots can be very useful when we want to testify multiple lines nicely. It enables us to evidence multiple trends in one graph, which saves the problem of designing more graphs and too adds to the aesthetic (this is a bit of personal stance). We apply the electricity consumption data in the US every bit an example, the 3d line plot helps to demonstrate the trend of electricity usage according to years and months in the aforementioned graph.
# plot of the electricity usage in the US
information.us <- usmelec
dmn <- listing(month.abb, unique(floor(time(data.us))))
# convert to data frame by month, to make data retrieval easier
res.us <- every bit.data.frame(t(matrix(data.u.s.a., 12, dimnames = dmn))) # ready the values of the 3d vectors
north <- nrow(res.us)
x.us <- rep(month.abb, times=due north)
y.us <- rep(rownames(res.us), each=12) z.u.s. <- as.numeric(data.us)
# we need to append 2 values to the vector
# converted from the time serial and we let them
# equal to the last value in the time series so the
# shape of the graph will non be influenced
north.z <- length(z.us)
z.usa[north.z+ane] = z.us[n.z]
z.us[northward.z+ii] = z.u.s.[north.z] data.us <- data.frame(x.us, y.u.s.a., z.usa)
colnames(data.united states) <- information.frame("x", "y", "z") fig.u.s. <- plot_ly(information.us, x = ~y, y = ~x, z = ~z,
type = 'scatter3d', mode = 'lines', color=~y.us)
# to plow off the warning caused past the RColorBrewer
suppressWarnings(print(fig.us))
In this example, the data is stored as a time series, which takes a bit of endeavor to set up the value of ten-, y- and z-axes. Fortunately, this is can be done simply using rep part.

From the y-z airplane, we can see that from 1973 to 2010, people are generally using more and more electricity, and from the x-z aeroplane, we can see how the electricity usage is distributed throughout the yr (this is in fact so-called seasonality, a very of import property possessed by some time series).
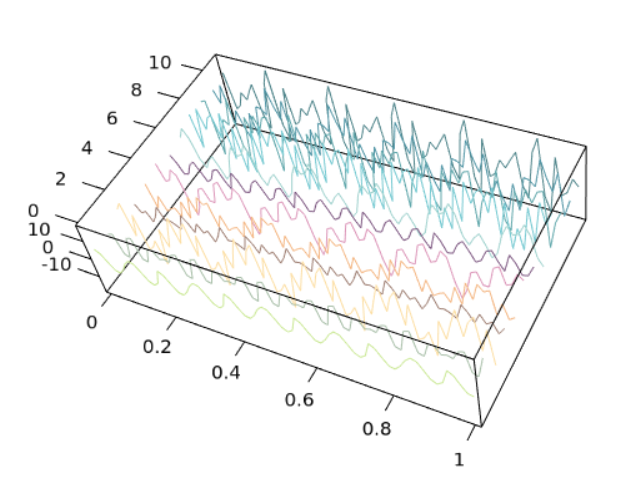
A waterfall plot (information technology'southward unlike from 3D line plots since in a 3D line plot there doesn't accept to be multiple lines — there can simply be a unmarried line going across 3D space) is a 3D plot, where multiple curves are shown simultaneously. Ordinarily, it is used to display spectra, e.g., to show the result of discrete Fourier transform. In R this tin can be realized using lines3d. The following code produces the plot of frequency components of a ten-element array afterward a complex Fourier transform.
# For displaying the result
options(rgl.printRglwidget = TRUE) x.f <- c(5, iv.2, nine, 3, 5.v, 8.2, 4.8, 6.4, xi, 10.2, eight.9, 10.9)
res.f <- fft(10.f) nx <- length(10.f)
ny <- seventy xx <- seq(0, nx, by = 1)
yy <- seq(0, 1, length = ny) aspect3d(4, 2.v, 1)
axes3d() cols <- c("#CBE896", "#AAC0AA", "#FCDFA6", "#A18276", "#F4B886", "#DD99BB", "#7F5A83", "#A1D2CE", "#78CAD2"
, "#62A8AC", "#5497A7", "#50858B")
for (i in 1:nx) {
c <- x.f[i]
a <- Im(res.f[i])[1]
b <- Re(res.f[i])[1]
lines3d(yy, 20[i], c*(sin(a*xx) + cos(b*xx)), col=cols[i], lwd=2)
}
The output of the above code is shown in Figure 2.2. For the code to run, the library rgl is necessary. Different the example before this (Figure 2.one), the lines are added 1 past i in a loop, instead of setting the locations of the points in the 3D space correct away.
We can use waterfall plots to display density as well. This can be achieved by the part slicedens, which is available from the GitHub repository BivariateSlicer. We can use thesource function to import the whole source file correct away, merely some of the examples included might not run properly. Therefore, it's better to just run the role. slicedens enables us to brand slices in the data and nowadays them in one 3D plot.
We utilize the Ames Housing Dataset equally an example, which is available from Kaggle.
housing <- read.csv2(file='data/AmesHousing.csv', header=True, sep=',')
housing
summary(housing$Gr.Liv.Area)
ground <- housing$Gr.Liv.Area
price <- housing$SalePrice plot(ground, price, cex=.2, col="deepskyblue3", xlab="Above grade living area", ylab="Toll") fcol <- c(.iii, .8, .8,.12)
lcol <- c(0.1, 0.5, 0.4,.1)
slicedens(ground,cost,
fcol=fcol, bcol='white', lcol=lcol,
gboost=0.015)
Expressed in a scatter plot, the data looks like Figure 2.four
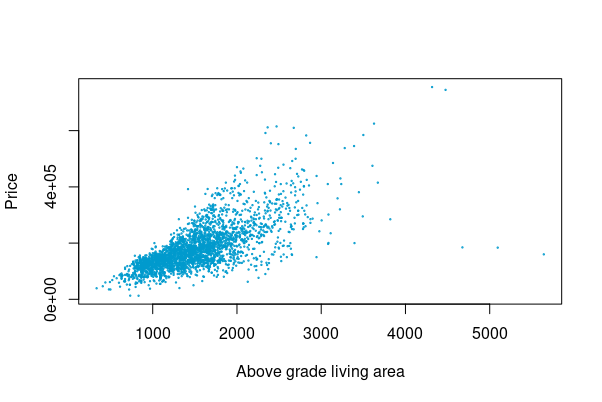
Imagine the scattered data is cut into several horizontal pieces, some of them contain more points, some less. Subsequently arranging the slices into a single plot, the result is displayed in Effigy 2.5.
The plot in Figure two.5 looks very nice, simply this might not exist the optimal way to nowadays scatter data. Nosotros can come across the density distribution from this effigy of course but compared with Figure 2.4, Figure 2.5 doesn't seem to be so clear — we can't make up one's mind which area and the cost range is most frequent. In this case, a second scatter plot similar Figure 2.4 might be improve. But because of the squeamish visual effect and the interesting thought of slicedens, this 3D plot is besides introduced in this article.
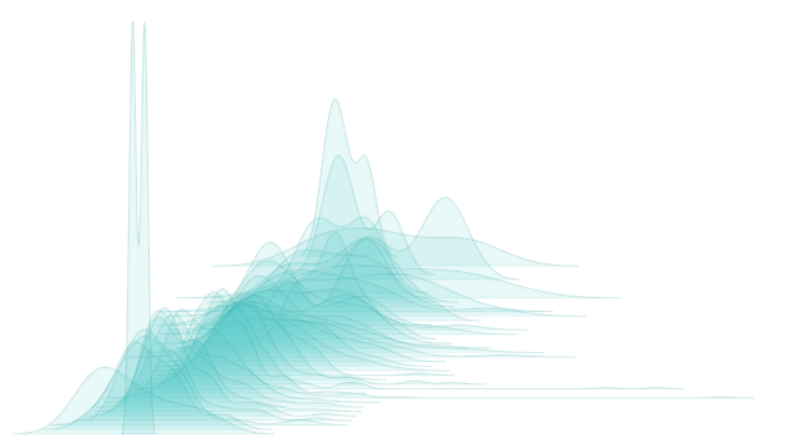
3d scattered plot
Scatter plots are a good way of presenting discrete observations. We use Edgar Anderson's Iris information equally an example, which gives the lengths and widths of sepal and petal of three species of iris. This is besides typically used for demonstrating PCA (Master component analysis). We will use the following lawmaking to make a scatter plot of the features of the flowers and the vectors of the components altogether. The code is a modified version of this. Don't worry if you don't know much nigh PCA, the math behind it will take some fourth dimension to explicate but the idea is simple — it is a technique that helps with reducing the number of dimensions of the dataset with minimum loss of data.
# iris data
summary(iris)
iris$Species <- gene(iris$Species,
levels = c("versicolor","virginica","setosa"))
pca <- princomp(iris[,one:4], cor=Truthful, scores=TRUE) # Scores
scores <- pca$scores
x <- scores[,1]
y <- scores[,two]
z <- scores[,3] # Loadings
loads <- pca$loadings scale.loads <- 3 p <- plot_ly() %>%
# the scatter plot of the data points
add_trace(x=10, y=y, z=z,
type="scatter3d", way="markers",
mark = list(color=y,
colorscale = c("#FFE1A1", "#683531"),
opacity = 0.7, size=ii)) ns <- rownames(loads)
# add the vectors of the components
for (k in 1:nrow(loads)) {
x <- c(0, loads[1000,1])*scale.loads
y <- c(0, loads[g,ii])*scale.loads
z <- c(0, loads[one thousand,iii])*scale.loads
p <- p %>% add_trace(ten=x, y=y, z=z,
blazon="scatter3d", style="lines",
line = list(width=8),
opacity = 1, name=ns[k])
}
# display the graph
print(p)
A 3D scatter plot can very well help us come across the distribution of the data and what role the "components" play.
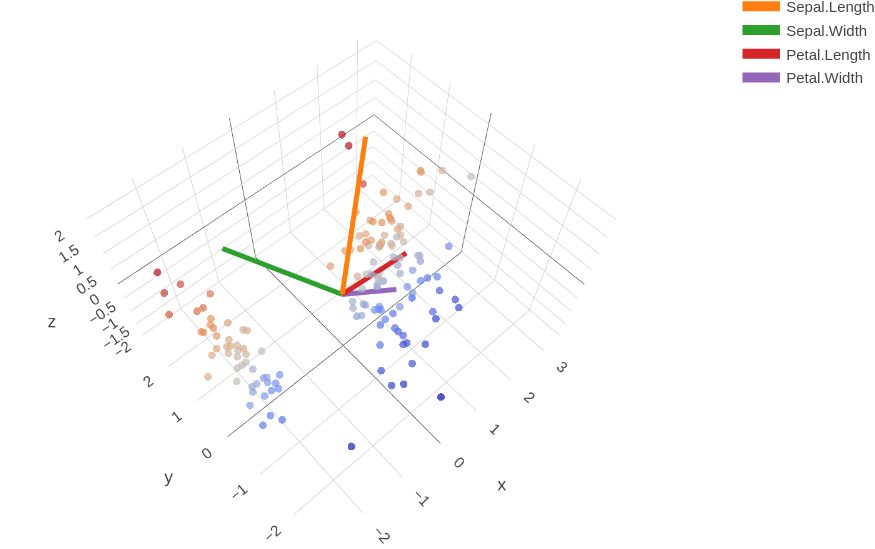
In Figure 3.ane, the data is non clustered (colored by the species), the colour simply changes along the y-axis. To plot clustered data, we tin can do information technology using the part plot_ly very easily.
p <- plot_ly(iris, x=~Sepal.Length, y=~Sepal.Width,
z=~Petal.Length, color=~Species) %>%
add_markers(size=ane)
print(p) 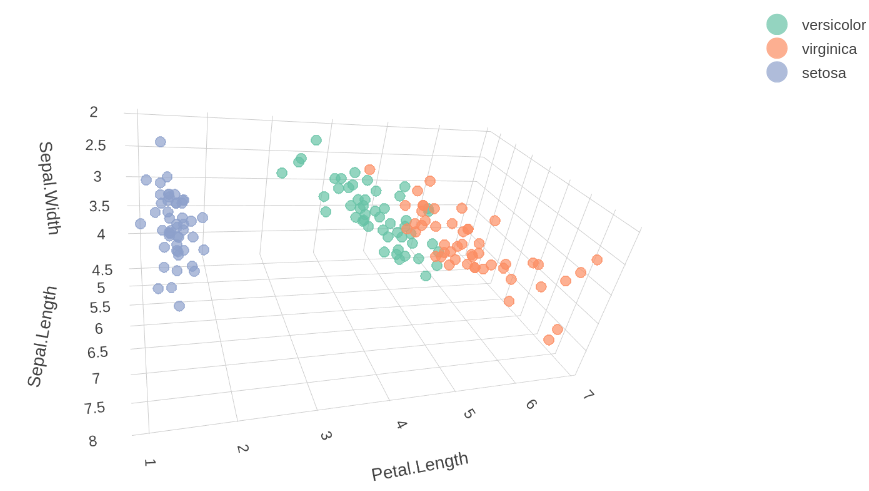
Other useful 3D plots
In this department, we introduce some other plots with code available.
(1) The fancy 3D histograms from: http://www.sthda.com/english language/wiki/impressive-parcel-for-3d-and-4d-graph-r-software-and-data-visualization, which is a nice tool for displaying the frequency of detached information, eastward.k. the number of seismic events with regard to longitude and latitude (Figure 3.3). In Figure 3.3, the columns announce the counts of seismic events in each range of longitude and latitude (the small squares in the x-y plane). On the 10-y airplane beneath the grids, the projection is the scatter plot of the depths of the seismic events in the given ranges.
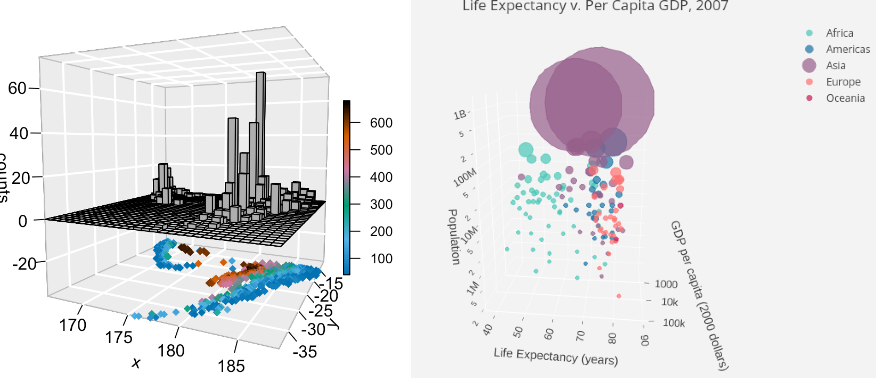
(ii) The 3D bubble plot from: https://plotly.com/r/3d-scatter-plots/. Information technology tin exist used to show the relation of multiple variables in a single 3D plot. The example given in Figure 3.four shows the human relationship between population, life expectancy, GDP, and countries (the label of every marking, information technology is visible when hovered over) too every bit land sizes (the size of the markers).
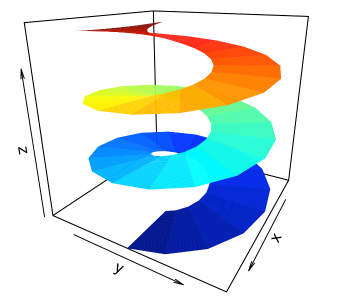
(iii) 3D surface plots for developing geometric intuition from: https://rviews.rstudio.com/2020/12/14/plotting-surfaces-with-r/. The examples from this article are very practical for visualizing topological shapes.
Source: https://towardsdatascience.com/make-beautiful-3d-plots-in-r-an-enhancement-on-the-story-telling-613ddd11e98
Post a Comment for "how to draw 3d graph in r"